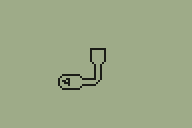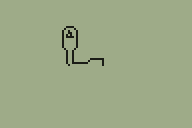Adapting a room from DOOM's E2M7 to the TI-83+ calculator
Thursday, 28th October 2010
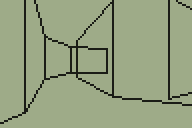
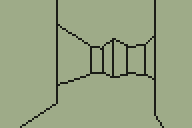
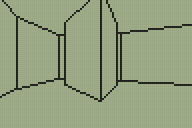
The level I've been working with as a test for the TI-83+ 3D engine was something I quickly threw together. I've never been much good at the design side of things, and my lack of imagination was producing something very simple that wasn't really challenging the engine and testing whether it could be used in a game. Looking for inspiration, I played through map E2M7 in DOOM and found a fairly interesting room to try to convert.

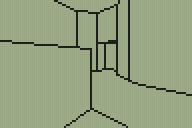

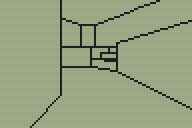

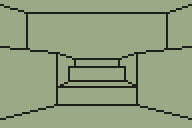

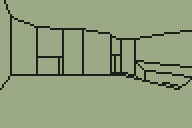

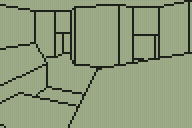
I'm sure you can tell which is the original room from DOOM and which is my adaptation of it.
Since the last post I have had to make quite a few tweaks to the engine. In the previous build there was a bug which cropped up when the top or bottom edges of walls appeared above or below the screen bounds. This turned out to be caused by a routine that was intended to clip a signed 16-bit integer to the range 0-63; it would return 0 for values 128 to 255 instead of 63. Fortunately this was an easy fix.
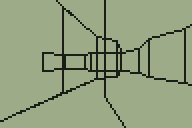
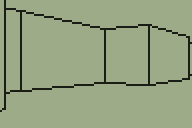
Another bug was in the way "upper and lower" walls were handled. Sectors have different heights and "upper and lower" walls go between two adjacent sectors and connect the ceiling of one to the other and the floor of one to the other, leaving a gap in the middle.
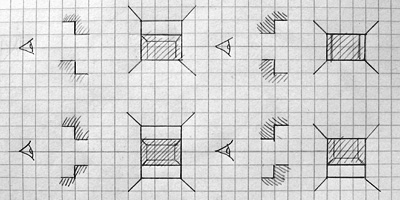
The above picture shows the four main types of sector-to-sector transition through an "upper and lower" wall type. Different transitions require different numbers of horizontal wall edges to be traced; in the bottom left example (going to a sector that has a lower ceiling and higher floor than the current one) four lines would be required and in the top right example (going to a sector that has a higher ceiling and lower floor than the current one) two lines would be required. The previous version of the engine always drew four lines, which would produce a spurious line above or below the "hole" for three out of the four different combinations of sector-to-sector transition. By comparing sector heights the right number of horizontal lines can be drawn, which greatly improves the appearance of the world and slightly increases the performance, too.
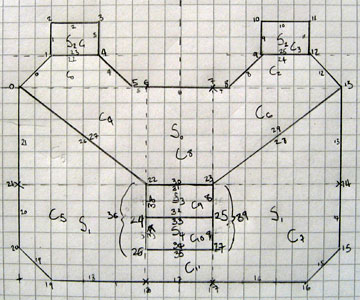
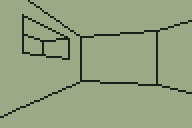
A less immediately obvious limitation was in my implementation of the BSP tree structure. Each node on the tree splits the world geometry into two halves; one half is in "front" of the partition and the other is "behind" it. Each chunk of split geometry can be further subdivided by additional partitions until you're left with a collection of walls that surround a convex region. You can then walk the tree, checking which side of each partition you are on to determine the order that the walls should be rendered in. For more detailed information the Wikipedia article on binary space partitioning is a good starting place but the basic requirement is that you should be able to slice up level geometry into convex regions with partitions. I had naïvely assumed that horizontal or vertical partitions would be sufficient (and they are useful as you can very quickly determine which side of a horizontal or vertical line the camera is on). However, this room demonstrated that such a limitation would not be practical.
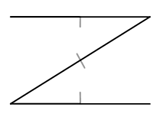
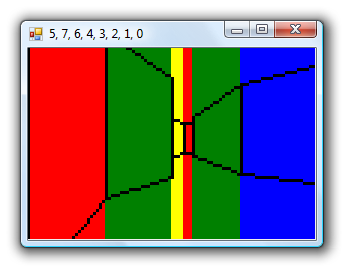
Consider the above geometry. The black lines are walls and the small grey lines represent the wall normals; that is, the walls face the inside of the "Z". The wall in the middle is double-sided; you could put the camera above or below it and see it. However you slice that map up with horizontal or vertical partitions you will still end up with regions that are not convex.
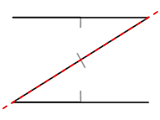
A single partition along the central wall divides the map into two convex regions. I had initially thought that checking which side of such a partition the camera lay would be an expensive operation, but it's not too bad; as a line can be represented by the expression y=mx+c I can store the gradient m and y-intercept c in the level data and simply plug in the camera's x and compare to y to determine the side. A single multiplication and an addition isn't too much to ask for.
Fortunately, there are only two of these partitions in the level!
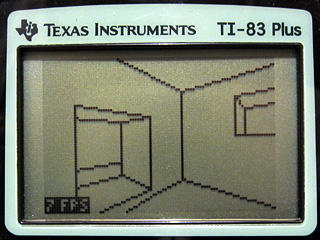
I have added some other features to the demo program. Pressing Zoom when using a calculator that can run at 15MHz (a TI-83+ SE or any TI-84+) toggles the speed between 6MHz and 15MHz. Pressing Mode or X,T,Θ,n allows you to look up or down. Pressing Window toggles between the default free movement and a mode which snaps you to a fixed height above the floor. These additions are shown in the below screenshot (click to view the animation):
Unfortunately, performance is lousy. Viewing the stairs drops the framerate to a rather sluggish 6 FPS when running at 6MHz (most of the above screenshot is recorded at 15MHz). The LCD's natural motion blur helps a little (it feels a lot more fluid on the calculator than it does on a PC emulator) but I'm aiming for a minimum of 10 FPS, so I need to make quite a few optimisations. There are several low-level ones that could be made; for example, when clipping the 2D line segments to the display I'm using a generic line clipper that clips the line both horizontally and vertically. As wall has been clipped to the horizontal field of view by that point I only really need to clip it to the top and bottom edges of the display. There are also some high-level optimisations to be made; for example, double-sided walls are currently stored as two distinct walls with the vertex order swapped. This means that to handle both sides of the wall the engine has to clip and project it twice, which involves lots of expensive divisions and multiplications. The results of these operations could be cached so that they only needed to be calculated once.
A TI-83 and TI-83+ binary is available if you'd like to try the demonstration on your calculator: please download Nostromo.zip. The usual disclaimers about backing up your data before running the program apply!
Varying wall heights in a 3D engine for the TI-83+
Monday, 25th October 2010
I've done a little more work on the 3D engine for TI-83+ calculators that I mentioned in the previous entry. The main difference is in limited support for varying the heights of floors and ceilings, illustrated in the following screenshots.
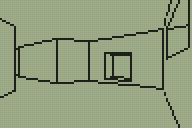
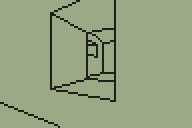
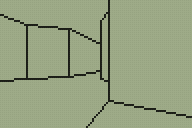
Walls now refer to one or two "sectors". A sector is a 2D region of the map of any size or shape; it can be concave or even have holes in it. Walls are also grouped into convex regions named subsectors for rendering purposes. Each wall has a sector in front of it and a sector behind it; these sectors have a specified floor and ceiling height. There are now two types of wall; a "middle" wall which connects the floor and ceiling of the sector in front of it and an "upper and lower" wall which connects the ceilings of the sectors on each side and the floors of the sectors on each side.
This makes occlusion a little trickier and determining where to draw lines around the edges of walls even more so!
The previous version of the renderer worked by drawing walls back-to-front, clearing rectangles the height of the screen behind the wall segments as they were drawn. The first attempt to improve this exchanged rectangles the full height of the screen with trapezia. The screenshot to the left shows the bounding rectangle around each wall segment being filled and the one to the right shows each wall filled as a trapezium. (As before, clicking an image with a border will display an animated screenshot).
Rather than attempt to calculate where lines should be drawn around wall edges I thought I'd experiment with dithered wall fills instead. The left screenshot shows this addition (each wall has a different shade) and the right screenshot shows the addition of support for wall heights (still drawn in the simple back-to-front technique, resulting in significant amounts of overdraw).

Unfortunately, the LCD on the calculator copes rather poorly with dithered fills; the above photograph was taken at the highest contrast setting. Rotating the camera to look at walls with a different dither pattern brings the world back into view. This is rather unacceptable, and is something I ran into with my previous implementation. I think I'll stick to stroked wall outlines rather than filled walls.
I had been experimenting with a new level design in the C# prototype of the engine that added another room accessible via a tunnel from the starting room. I added some code to the C# program to output the level data in a form that could be assembled into the Z80 version. This is shown above, having reverted to a simple wireframe view in anticipation of the new wall drawing code.
The new way to implement occlusion works very differently to the previous one. I had been sorting the geometry from back-to-front and rendering it in order, drawing walls in the foreground on top of walls in the background. This wasn't very efficient and wouldn't scale well. The new approach renders from the front to the back and works on information stored about each column of pixels on the screen. The screen is 96 pixels wide, so there are 96 columns to deal with. A counter is set to 96 at the start of rendering. When a column of a wall is rendered, a flag is set to indicate that that column has been completed and the counter is decremented. When the counter reaches zero, that means that every column on the screen has been completed and the renderer terminates. This is demonstrated in the above screenshot when compared to the previous one; walls that are some distance away from the camera (and behind other wall segments) are not always drawn as the renderer has decided that it has finished before reaching them.
An obvious issue with the above screenshot is that even though some of the geometry is culled, individual walls can still be seen through other ones.
Part of the solution is to use a custom line-drawing routine that checks each pixel against the completed columns table. If a column is marked as completed, the pixel is not drawn; if it isn't, the pixel is drawn. This is shown above.
I previously mentioned that there were two types of wall; "middle" walls (solid ones from the floor to the ceiling) and "upper and lower" ones (these have a hole in the middle). Only "middle" walls flag a column as being completed, as you need to be able to see through the hole in "upper and lower" ones. This causes the rendering bugs in the previous screenshot above and below the holes in the wall. The way to fix this is to add two new per-column clipping tables; one which defines the top edge of the screen and another which defines the bottom edge. These both start at the maximum values (0 for the top edge and 63 for the bottom) and are reduced whenever an "upper and lower" wall type is encountered.
The new code to do this is demonstrated in the above screenshot. There is still, however, a bug in this implementation. The per-column clipping tables are updated by the code that draws the line along the bottom or top edge of the hole in the wall. If this line is partially (or completely) off the screen, these tables are not updated and the rendering bugs appear again (as demonstrated at the end of the above screenshot). A final manual pass over parts of the line that are clipped off the screen corrects the issue:
As can be seen in the bottom left corner of the above screenshot I have added an FPS counter. This is accompanied by code that scales movement by elapsed time so you move at the same speed regardless of how long each frame takes to render. The engine is quite slow (and could no doubt be heavily optimised by someone who's good at assembly) and has quite a few bugs in it but it's certainly looking a little better than it did a week ago. As I only have a regular TI-83+ I'm aiming for something usable at 6MHz; the more modern calculators can run at 15MHz but this feature is not used in the demo.
For those interested in trying the demo on their calculators, click on the above image to download an archive containing a TI-83+ and TI-83 binary. As before, this is experimental and may well crash your calculator, so please back up any important files first!
A primitive 3D engine for the TI-83+
Sunday, 17th October 2010
As you may have guessed from the number of spinning cubes in my projects, I am quite fond of primitive 3D. As you may also have guessed from the number of TI-83+ calculator projects I have undertaken, I'm also quite fond of programming on low-end machines. I have never really successfully put 3D and the TI-83+ together, though.
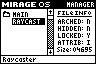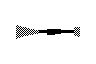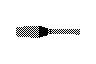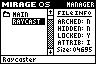
One way to build a 3D world in software is raycasting (e.g. Wolfenstein 3D). This typically results in blocky worlds where all walls are at 90° angles to each other. There are several games using raycasting engines on the TI-83+ already; they are much faster and better-looking than my sorry attempt pictured above.

Another method is to use true 3D geometry (e.g. Quake). Many years ago I attempted to work on something that looked a little like Quake. I built this on the Matt3D engine, which supported basic 8-bit coordinates and lines, but not solid objects. The result was even less useful than the above raycaster!

Another method somewhere between the two is a "2.5D" engine, where level geometry is defined between points in 2D space but projected in 3D (e.g. DOOM). This allows for walls that are not at 90° angles to each other, whilst simplifying the rendering procedure significantly. I spent some weeks working on such an engine a few years ago yet never managed to get any further than the above screenshot. As you can probably tell from the fact that you can see the walls through each other I never found a good way to handle occlusion, and the project ended up stagnating.
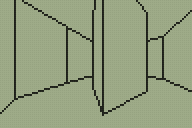
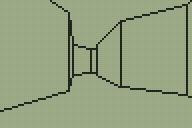
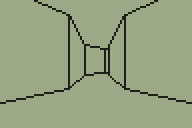
Looking for a quick weekend project I thought back to the work I'd done with the DOOM and Quake engines. These engines use a BSP tree structure to sort the level geometry for rendering. I reckoned that if simplified a little a similar tree structure could be used to render a 3D world on the TI-83+ calculator. The four screenshots above show that this technique is indeed quite successful. My implementation could certainly do with a lot of work but I think the theory is at least sound.
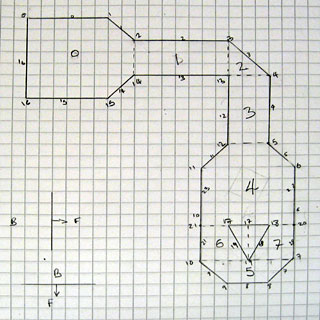
I decided that one way to make this project a bit more fun was to set myself a challenge; to design a level that I would, ultimately, be able to walk around in. This level is shown above, and contains a number of walls that are not parallel to the X or Y axis and a pillar. I have split the world into eight convex "sectors" (labelled 0 to 7) with a dotted line between them to show where the BSP tree is partitioned. All of the partitions are either horizontal or vertical to speed up tree traversal; the TI-83+'s Z80 CPU does not support floating point arithmetic, let alone multiplication or division, so being able to decide which side of a partition you're on quickly is very useful.
Rather than dive straight into Z80 assembly programming I knocked together a quick prototype in C#. This allows for quick and easy debugging; the blocks of colour allow me to quickly identify walls and the application title bar contains the order in which the sectors have been rendered. These can then be checked against the version running on the TI-83+ in case there are problems.
With the C# version running satisfactorily I started converting it to Z80 assembly. The above screenshot shows the first step; transforming the level's vertices around the camera. Clicking on the screenshots will take you to an animated version; as some of them are quite large I have linked to them rather than embedding them directly.
The next step was to traverse the BSP tree. The numbers across the top of the screen indicate the order in which to render the sectors, from back to front — however, due to a simple bug, they are actually listed from front to back. This was fortunately very easy to fix.
Walls are connected between the vertices, so I quickly threw something together to display all of the walls on the screen. The walls will have to be clipped against the camera's view (or discarded entirely if they are outside the view) so being able to see them is a great debugging aid!
We are only interested in drawing walls that are in front of the camera, so the first bit of clipping code deals with clipping the walls against Y=0.
The above screenshots show the final three stages of clipping to the camera's view, defined by Y>0, Y>+X and Y>-X. The first screenshot shows culling of any wall that does not satisfy this in any way; walls that are completely outside the view are discarded. The second screenshot shows walls being clipped against Y=+X, and the third finally adds clipping against Y=-X. The lack of hardware floating-point arithmetic makes the code fairly slow and ugly but it does seem to be working relatively well.
We are only really interested in dealing with walls that are facing the camera; we don't want to draw the back of walls. To work out which we want to keep and which we want to ignore, we project the wall to the screen and check whether its projected start vertex appears to the left or the right of its end vertex.
A simple perspective projection is performed to turn this clipped 2D world into what appears to be a 3D one. The X coordinate of each vertex is divided by its Y to get the X coordinate on-screen and the height of the wall is divided by the vertex Y to get the Y coordinate on-screen. The left screenshot shows the top and bottom of wall edges; the right screenshot adds lines between the floor and the ceiling to produce a more convincing "wireframe" view of the world.
The final step is to make the world appear solid, by hiding walls that are far away behind walls that are closer to us. Traversing the BSP tree gives us the order in which to draw the walls, so all that is required is to draw solid quadrilaterals for each wall rather than the lines around its outside. A fast clipped quadrilateral filler would take me some time to write so I cheated by drawing a solid white rectangle the width of the wall and the height of the entire screen before drawing the wall outlines. As the camera is half-way up each wall and all of the walls are the same height there are no cases where a foreground wall only partially covers a background one so this trick works for the time being.
I'm glad I achieved my goal of walking around the 3D world I'd sketched in pencil at the start of the weekend but I'm not sure where I'll be able to take the project now. Turning it into a useful 3D engine for a game would certainly require a lot of work. The level and its BSP tree were generated by hand, which would not lend itself well to anything but the simplest of levels. However, the lack of variation in wall heights produces fairly dull levels in any case; DOOM-style levels would be something to strive for, but I'm not sure how well the calculator would be able to cope with them. I'm also unsure how well the engine would scale; this very primitive version only achieves around 12 FPS on a 6MHz TI-83+. It's certainly given me something interesting to think about!
If you would like to try the program on your calculator, please download Nostromo.8xp. It requires an Ion-compatible shell to run. It is very primitive, likely to be quite buggy (you may encounter rendering bugs when very close to walls due to integer overflow in the clipping and projection code) and may well crash your calculator; please back up any important files before running it. Use the arrow keys to move around, Trace and Graph to strafe and Clear to quit.
TV Demonstrator for TI calculators
Monday, 11th October 2010
I've been tinkering with a number of small projects recently. I've resumed work on an LED clock for my bedroom (using a 32×8 LED display) and written an experimental BASIC interpreter in C# which I may try to turn into an assembler (implementing assembly statements as BASIC ones). In the mean time, I have finished one project — a device to display a calculator's screen on a television set.
Texas Instruments also manufacture a product that allows you to view the screen contents of a calculator with supported hardware on a TV; here is a video demonstrating it. The additional hardware (either on special "ViewScreen" calculator models or built into the more advanced calculators such as the TI-84+) allows the device to mirror what is sent to the calculator's LCD in real-time.
I do not have one of these calculators, just a plain old TI-83+. However, this calculator (as well as the older TI-83 and TI-82) allows you to capture a screenshot over the link port. Pressing a button on my device captures a screenshot in this manner and displays it on the TV. This relies on the calculator being in a state where it can respond to these screenshot requests, so is not ideal, but considering that the TI Presenter costs $300 and relies on special hardware inside the calculator and mine should cost less than a tenth of that in parts and work with older calculators I think it's a decent compromise.
I had previously believed that NTSC composite video signals used a negative voltage for sync pulses. I have since found documents that indicate that the sync, black and white levels are the same as those for PAL. The timing is, naturally, different but as there's no need to change the hardware it makes supporting both NTSC and PAL relatively straightforwards. This contraption can be set to operate in either NTSC or PAL mode by sending the real variable M to it from the calculator, with a value of 60 for NTSC and 50 for PAL.
I acknowledge that this is not the most useful of projects (unless you're a maths teacher with an interest in electronics) but the code may be of interest for other projects. A handful of inexpensive parts can get you a picture on a TV from a 96×64 monochromatic frame buffer (the 1KB RAM on the ATmega168 doesn't allow for much more, alas).
More information and downloads can be found on the TV Demonstrator project page.