Blobs

Smooth, fast morphing blobs which seem to be able to attract eachother and link up sound like they could be a challenge to code - but are in fact dead simple. Ridiculously so, actually!
Puzzling them out
I'll have to confess - that image at the top of the page is not a straight screenshot. It's a number of screenshots tiled together - in reality my demo only deals with 3 blobs, though it's easy enough to add more to it. So, what seems to be going on?
Let's ignore the blue glow around each blob for the moment and concentrate on the green body for the moment. Each pixel on the display seems to be coloured relative to the distance away from the centre of each blob it is. That is, a pixel that falls over the centre of a blob is bright, stays quite bright for a fair range over the surface of the blob then falls off very quickly towards the edges until it is dark.
Look closely at the picture again. The brightness is clearly not a linear relationship to the distance, else it would fall off smoothly, and not have that sharp cut-off point. We could clip it, so if it's less than (say) half brightness then we set it to black. However, that would lead to jagged pixel edges and unsmooth fades to black, and the edges here certainly fade smoothly to black.
The idea here is to use a relationship of the distance squared. "Ah", you might say, "that would still leave us with fuzzy blobs". What we need to do is use a pretty sharp curve and clip the range of brightnesses. Here's a sketch of what I mean: note that the curve is flipped upside down to how you'd normally see a graph of y = x2.
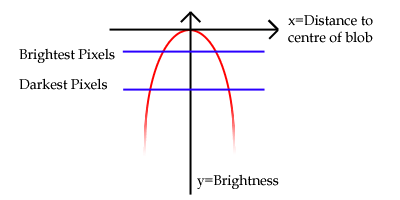
The red curve is our distance2 curve. The vertical y axis indicates the overall brightness. The horizontal x axis indicates the distance from the pixel to the centre of a blob, with the point where they cross being the brightest (distance = 0). We clip the brightness returned between a minimum and a maximum value - demonstrated here by the two blue lines.