A larger level, moving sectors and failed optimisation attempts
Monday, 29th November 2010
I've made a few attempts to boost the performance of the 3D engine for the TI-83+ I'm working on with little success. I had previously failed to get any improvement by adding bounding boxes around each BSP node (the idea being that if a node falls outside the view you can discard it and, by extension, all of its children) but the act of transforming the bounding box to determine whether it was inside or outside the view was more CPU intensive than blindly handling the nodes whether they were inside the view or not.
A simpler test, I reckoned, would be to use bounding circles. These only have one point to transform, and determining whether they are in the view is one comparison to ensure that they're in front of the camera followed by one multiplication (by the constant √2) and two more comparisons to determine whether they are to the left or right of the camera's view; far simpler than a bounding box!
The bounding circles did cut down the number of BSP nodes that were handled each frame but the additional checks made the engine slightly slower in general than it had been before. In some circumstances it was slightly faster, but not enough to make a noticeable difference. The additional data per BSP node added over 900 bytes to the level data, too, so the attempted optimisation had to go.



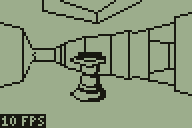



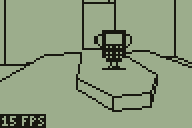
The newly added rooms to the demo level
One tweak that did boost performance noticeably was to cache the projected X coordinate of each vertex. All vertices in the map have at least two walls connected to them and so are projected to the screen at least twice if within the view. I already had a table that was used to indicate whether a vertex had been transformed around the camera or not that frame so it was easy enough to add the X coordinate of the projected vertex to that table, adding around a 15% boost to the framerate.
Points are projected to the screen by dividing their X (left/right) or Z (up/down) component by their Y (depth) component. Division is slower than multiplication so I tried to calculate the reciprocal of the depth for the vertex then perform all subsequent projection operations by multiplying the X or Z component by this reciprocal. Unfortunately, this resulted in a lack of precision owing to my use of 16-bit fixed-point numbers (walls "wobbled" as you moved the camera) and performance was about the same as it had been before, so I rolled back the changes.
The block of screenshots in the above text shows a new region that has been added to the demo level, and the image below is a map of that level — fans of DOOM may notice that it's based on a small portion of E2M7 (The Spawning Vats).
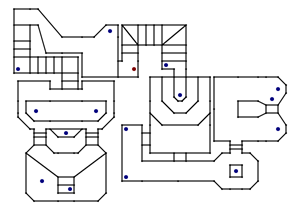
Map of the level
This level now uses every one of the 256 walls that are available, so is probably a good indication of the maximum size of a single level (and at 6,626 bytes it's certainly rather taxing on the limited amount of memory in a TI-83+ calculator).
This is, however, the maximum size of a single level. It does not take long to load and unload levels, so it would be quite possible to construct a continuous level that appears larger by unloading the current one and loading a different one when the user moves to a particular region. This could be implemented in an obvious manner (such as the player stepping into a teleporter) or transparently (by moving the player into an identical copy of the room he left to hide the transition). The latter option also introduces the option of level geometry that would otherwise be impossible in a 2D-based engine, such as rooms above rooms. Special effects could also be tried, such as an infinite corridor that warps you back to the beginning when you reach its end.

However this feature is implemented, there would need to be some way to trigger the action. The above animated screenshot demonstrates the current trigger system which is used to set a sector in motion. A sector, in this instance, is a region with a particular floor height and ceiling height. Each wall indicates which sector is in front of it and which sector is behind it. Convex sub-sectors contain sets of walls and also indicate which sector they are part of, and are attached to the leaves of the BSP tree. Given a point, you can quickly find out which convex sub-sector it is in by walking the BSP tree. When you have found the convex sub-sector you can then look up its sector. This is currently used to set the player's height, as the sector tells you the floor height.
If you keep track of the player's sector each frame you can tell when they have moved from one sector to another. This then fires an event, reporting which sector the player used to be in and which they are in now. In the above screenshot, the platform is set to descend whenever the sector surrounding it is entered from any sector other than the platform itself (this is to stop it from automatically descending when the player walks off the top of the raised platform). It is also set to rise whenever the platform's own sector is entered. This produces a simple lift; doors are handled in a similar fashion elsewhere in the level.
If you'd like to try this demo on your calculator, you can download the binaries for the TI-83 and TI-83+ in Nostromo.zip. As ever, please back up any important files on your calculator before running the demo; it may well clear your RAM. For those without calculators, an animated screenshot is available.