Clipping works! (Almost)

Monday, 3rd July 2006

Clipping now works in nearly all cases:

One of the problems was lack of precision. Here's the typical case that worked, running in my mockup:

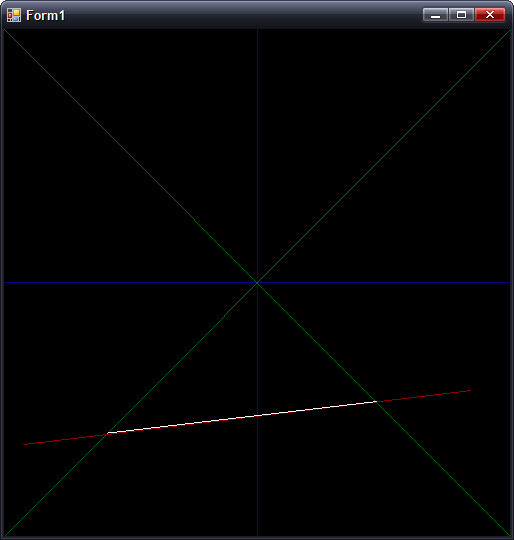
In this case, where |dX| > |dY|, all is good. However, switch that around so that |dY| > |dX|, and you get the following:

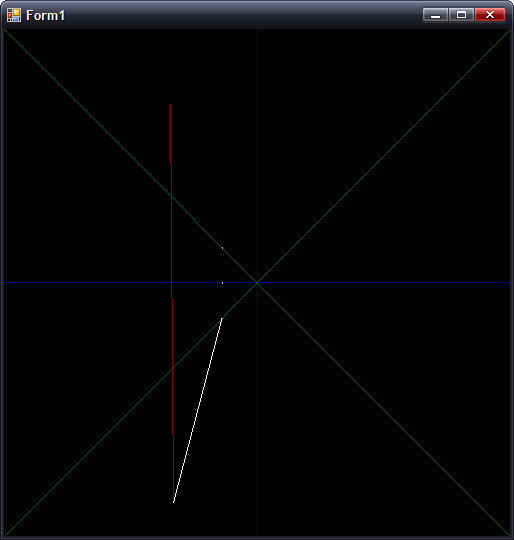
(Fixed point isn't so good for holding values that tend towards infinity). The solution is to have two branches for the clipping arithmetic, switching to the alternative form when |dY| > |dX|.

Preparation:
m = (Y₁ - Y₀) ÷ (X₀ - X₁) ; m is negative gradient.
c = Y₀ + m × X₀ ; Not sure what to call this, but it's used in all the below calculations

Clipping to y = 0:
x = c ÷ m
y = 0

Clipping to y = +x:
y = c ÷ (1 + m)
x = +y ; not used as we can skip having to transform.

Clipping to y = -x:
y = c ÷ (1 - m)
x = -y ; not used as we can skip having to transform.

The reason for clipping to y = 0 is to make sure the line is clipped to the correct side.

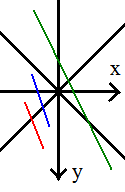
If you look at the red and blue lines, you can see that the far out-of-range points both have x < 0. This indicates that you should clip to y = -x. However, the green line also has the far end at x < 0, but we actually need to clip to y = +x. We can fix this problem by first clipping to y = 0, then checking the sign of x.

To fix the steep gradient problem, I just need to switch to these alternative sums:

First up, the gradient and c are calculated as:

m = (X₀ - X₁) ÷ (Y₁ - Y₀) ; Flipped
c = X₀ + m × Y₀ ; Again, X/Y flipped.

For clipping to y = 0:
x = c ; No need to divide by m!

The only other difference is to make sure that when clipping y = -x:
y = c ÷ (m - 1) ; as opposed to (1 - m)

...and all is hunky-dory.

The only remaining problem is if you are positioned directly inside a wall, which collision detection should fix.