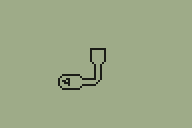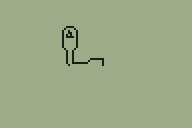A larger level, moving sectors and failed optimisation attempts

Monday, 29th November 2010

I've made a few attempts to boost the performance of the 3D engine for the TI-83+ I'm working on with little success. I had previously failed to get any improvement by adding bounding boxes around each BSP node (the idea being that if a node falls outside the view you can discard it and, by extension, all of its children) but the act of transforming the bounding box to determine whether it was inside or outside the view was more CPU intensive than blindly handling the nodes whether they were inside the view or not.

A simpler test, I reckoned, would be to use bounding circles. These only have one point to transform, and determining whether they are in the view is one comparison to ensure that they're in front of the camera followed by one multiplication (by the constant √2) and two more comparisons to determine whether they are to the left or right of the camera's view; far simpler than a bounding box!

The bounding circles did cut down the number of BSP nodes that were handled each frame but the additional checks made the engine slightly slower in general than it had been before. In some circumstances it was slightly faster, but not enough to make a noticeable difference. The additional data per BSP node added over 900 bytes to the level data, too, so the attempted optimisation had to go.

        

        

        

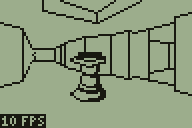
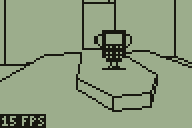
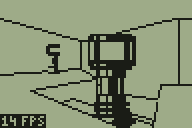
The newly added rooms to the demo level

One tweak that did boost performance noticeably was to cache the projected X coordinate of each vertex. All vertices in the map have at least two walls connected to them and so are projected to the screen at least twice if within the view. I already had a table that was used to indicate whether a vertex had been transformed around the camera or not that frame so it was easy enough to add the X coordinate of the projected vertex to that table, adding around a 15% boost to the framerate.

Points are projected to the screen by dividing their X (left/right) or Z (up/down) component by their Y (depth) component. Division is slower than multiplication so I tried to calculate the reciprocal of the depth for the vertex then perform all subsequent projection operations by multiplying the X or Z component by this reciprocal. Unfortunately, this resulted in a lack of precision owing to my use of 16-bit fixed-point numbers (walls "wobbled" as you moved the camera) and performance was about the same as it had been before, so I rolled back the changes.

The block of screenshots in the above text shows a new region that has been added to the demo level, and the image below is a map of that level — fans of DOOM may notice that it's based on a small portion of E2M7 (The Spawning Vats).

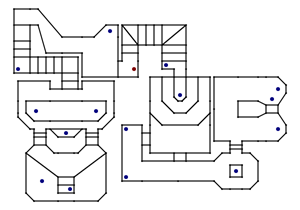
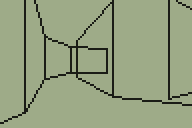
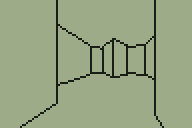
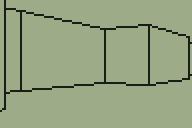
Map of the level

This level now uses every one of the 256 walls that are available, so is probably a good indication of the maximum size of a single level (and at 6,626 bytes it's certainly rather taxing on the limited amount of memory in a TI-83+ calculator).

This is, however, the maximum size of a single level. It does not take long to load and unload levels, so it would be quite possible to construct a continuous level that appears larger by unloading the current one and loading a different one when the user moves to a particular region. This could be implemented in an obvious manner (such as the player stepping into a teleporter) or transparently (by moving the player into an identical copy of the room he left to hide the transition). The latter option also introduces the option of level geometry that would otherwise be impossible in a 2D-based engine, such as rooms above rooms. Special effects could also be tried, such as an infinite corridor that warps you back to the beginning when you reach its end.

However this feature is implemented, there would need to be some way to trigger the action. The above animated screenshot demonstrates the current trigger system which is used to set a sector in motion. A sector, in this instance, is a region with a particular floor height and ceiling height. Each wall indicates which sector is in front of it and which sector is behind it. Convex sub-sectors contain sets of walls and also indicate which sector they are part of, and are attached to the leaves of the BSP tree. Given a point, you can quickly find out which convex sub-sector it is in by walking the BSP tree. When you have found the convex sub-sector you can then look up its sector. This is currently used to set the player's height, as the sector tells you the floor height.

If you keep track of the player's sector each frame you can tell when they have moved from one sector to another. This then fires an event, reporting which sector the player used to be in and which they are in now. In the above screenshot, the platform is set to descend whenever the sector surrounding it is entered from any sector other than the platform itself (this is to stop it from automatically descending when the player walks off the top of the raised platform). It is also set to rise whenever the platform's own sector is entered. This produces a simple lift; doors are handled in a similar fashion elsewhere in the level.

If you'd like to try this demo on your calculator, you can download the binaries for the TI-83 and TI-83+ in Nostromo.zip. As ever, please back up any important files on your calculator before running the demo; it may well clear your RAM. For those without calculators, an animated screenshot is available.

Enlarging the world

Sunday, 7th November 2010

There have been very few changes to the features of Nostromo recently. I have tried a number of ways to optimise the performance and whilst the handful of micro-optimisations I have made have boosted the frame rate a little none of the higher-level optimisations have done much. I did try, for example, storing a bounding box around each BSP node and ignoring it (and all its children) should this bounding box fall outside the field of view; the additional code to check the bounding box ended up halving the framerate rather than improving it.

        

        

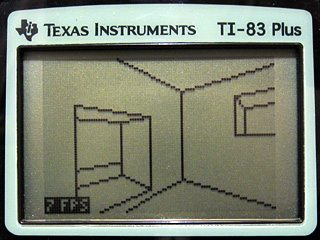
I have, however, enlarged the level quite considerably. A staircase connects the central room with the pit to a rather strangely-shaped arrangement of walls (again copied from E2M7). The room with a pit continues to cause issues; looking across it towards the room with the small central staircase forces the engine to step through a very large number of convex sub-sectors and check many walls. This drops the frame rate down to about 3 FPS on a TI-83+. However, this is specific to that room; the newly-added rooms have not noticeably affected the frame rate in other parts of the level.

Another minor improvement is that the engine now supports different sprites. I'm not too good at drawing them, as you can probably tell from the above screenshots, but at least the code is there to support them.

You can download a TI-83 and TI-83+ binary to try the demo on your calculator (please back up any important files first). Alternatively, here is an animated screenshot.

Adding sprite objects to the 3D world

Tuesday, 2nd November 2010

The previous entry showed a room from a map copied from DOOM's E2M7. I have since added the adjacent room:

    

    

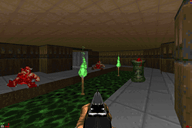
It may not look as interesting as the other room but it is significantly more costly to render due to the sheer number of lines visible at a time in it. Looking across it from the far corner dropped performance down to around 2 FPS on the 6MHz TI-83+, which was really not a very good effort. I spent a fair amount of time over the weekend trying to optimise the code as much as I could, and manage to bring the frame rate in the player's starting position from 6 FPS up to the target 10 FPS. Looking across the length of the new room still dropped the framerate to around 4 FPS at 6MHz, but it's a start.

Once the engine had been made a little faster it seemed a good idea to slow it back down again by adding a feature. I had been pondering how to add objects in the form of scaled sprites to the world. Working out where to put them on the screen isn't so difficult, but clipping them against the world geometry so that they couldn't be seen through walls is another matter entirely. One way that seemed popular is to draw the objects in reverse depth order (drawing the sprites that were further away before those that were closer) and using a depth buffer for the world geometry to clip each pixel of the sprite against the world. This would take up a lot of memory on the calculator and run very slowly (populating the buffer with a depth value for each pixel would be a very expensive operation, as you'd have to interpolate depth values between the ends of walls and edges of floors).

The engine makes use of three per-column clipping tables when rendering the scene. One keeps track of columns that have been completed (usually by drawing a "middle" wall to that column); once completed no more pixels may be drawn to that column. The other two tables are used to define the upper and lower clipping bounds. At the start of the scene these are reset to the top and bottom edges of the display. As the world is rendered from front-to-back these regions are reduced to clip geometry that is further away against geometry that is nearer (think of looking through a hole in a wall — things that are further away from you will never be drawn in the space above or below that hole).

Fortunately, you can use this clipping information to clip sprites against the world geometry too. Each sprite object needs to be associated with a convex subsector. These subsectors are made up of walls and are drawn from front-to-back (sorted by the BSP tree) as the world is rendered. Before each one of these subsectors is drawn it is checked to see if it contains any sprite objects — if it does, the current clipping buffers and a reference to the subsector are pushed onto a stack. When all of the walls and floors have been drawn this stack contains a list of all of the subsectors containing sprites and the clipping regions used to draw those subsectors in front-to-back order. Stacks are Last In, First Out structures and so when you pull the data back out of this stack you end up retrieving a list of sprites to draw and the associated clipping regions in back-to-front order. This allows you to effectively unwind the clipping operations, so as you draw the sprites from back-to-front you can gradually enlarge the clipping regions in the opposite order to the way that they were reduced when drawing the walls. You would still need to sort the sprites manually from back-to-front within each subsector, but for the time being I've limited myself to one sprite per subsector for ease of development.

    

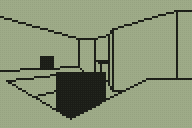
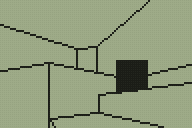
The above screenshots demonstrate an initial test of the "things" (as they are apparently technically called), rendering them as solid black squares.

    

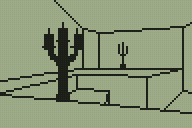
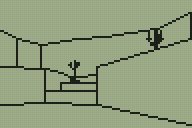
Scaled sprites tend to be more useful than solid black squares, however, so here are a pair of candlesticks (well, that was the intention at any rate; call them cacti if you must). The sprite was simply ORed to the display, so pixels could be black or transparent.

I then added support for "white" pixels too. The above screenshot is a link to an animated GIF showing the engine in action. The sprites appear to jiggle up and down and have invalid data drawn underneath them in places, which was caused by my accidentally overwriting an important register before rendering each column (fortunately an easy one to spot)! The relatively high frame rate in the above image was helped by running at 15MHz and using the old single-room map.

The above screenshot (click for the animated GIF) fixes the dancing sprites and restores the second room, though is still running at 15MHz. For a bit of fun I added animated doors; all this does is adjust the floor heights of the sectors used to represent "doors" (pressing Alpha will toggle both doors open or shut) but it makes the world look a little more dynamic.

There are still some rendering bugs in the engine. The above animated screenshot demonstrates one; when close to a wall edge you will sometimes see a temporary vertical line the height of the screen or the screen will flash white. I reckon this is probably an integer overflow issue causing the projected height of a line to be on the opposite side of the screen than the one it should be (the bottom edge of a hole in a wall may be projected above the screen rather than below it, causing the entire screen to be clipped out, for example). One bug that took a while to identify (it only appeared in very particular positions; moving one unit in any direction cured it) was caused by truncating a 32-bit integer to a 24-bit one. When viewing a long wall from a long distance the result of a 16-bit (difference between end and start X coordinates) by 16-bit (Y coordinate of the start of the wall) multiplication was resulting in a value of $00800000 or so (a large positive number). When truncated to 24 bits this becomes $800000, which has the most-significant bit set and was therefore treated as a large negative number. As this was part of the wall clipping code it would end up clipping a wall end a long way behind the camera instead of within the view; fortunately this obvious mistake is easy to spot and correct (the answer can only be positive, so if you get a negative one just negate it).

If you'd like to try the demo on your own calculator please download Nostromo.zip. As this is a work in progress there are likely to be bugs so please back up any important files first!

Adapting a room from DOOM's E2M7 to the TI-83+ calculator

Thursday, 28th October 2010

The level I've been working with as a test for the TI-83+ 3D engine was something I quickly threw together. I've never been much good at the design side of things, and my lack of imagination was producing something very simple that wasn't really challenging the engine and testing whether it could be used in a game. Looking for inspiration, I played through map E2M7 in DOOM and found a fairly interesting room to try to convert.

    

    

    

    

    

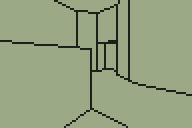
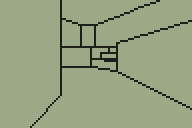
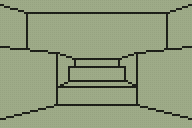
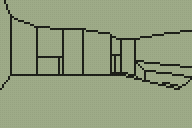
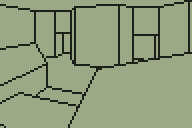
I'm sure you can tell which is the original room from DOOM and which is my adaptation of it.

Since the last post I have had to make quite a few tweaks to the engine. In the previous build there was a bug which cropped up when the top or bottom edges of walls appeared above or below the screen bounds. This turned out to be caused by a routine that was intended to clip a signed 16-bit integer to the range 0-63; it would return 0 for values 128 to 255 instead of 63. Fortunately this was an easy fix.

Another bug was in the way "upper and lower" walls were handled. Sectors have different heights and "upper and lower" walls go between two adjacent sectors and connect the ceiling of one to the other and the floor of one to the other, leaving a gap in the middle.

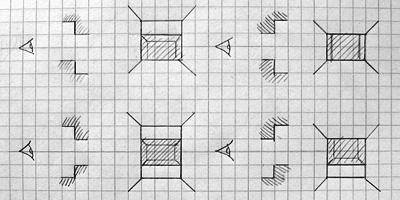
The above picture shows the four main types of sector-to-sector transition through an "upper and lower" wall type. Different transitions require different numbers of horizontal wall edges to be traced; in the bottom left example (going to a sector that has a lower ceiling and higher floor than the current one) four lines would be required and in the top right example (going to a sector that has a higher ceiling and lower floor than the current one) two lines would be required. The previous version of the engine always drew four lines, which would produce a spurious line above or below the "hole" for three out of the four different combinations of sector-to-sector transition. By comparing sector heights the right number of horizontal lines can be drawn, which greatly improves the appearance of the world and slightly increases the performance, too.

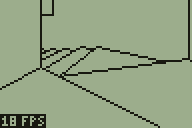
A less immediately obvious limitation was in my implementation of the BSP tree structure. Each node on the tree splits the world geometry into two halves; one half is in "front" of the partition and the other is "behind" it. Each chunk of split geometry can be further subdivided by additional partitions until you're left with a collection of walls that surround a convex region. You can then walk the tree, checking which side of each partition you are on to determine the order that the walls should be rendered in. For more detailed information the Wikipedia article on binary space partitioning is a good starting place but the basic requirement is that you should be able to slice up level geometry into convex regions with partitions. I had naïvely assumed that horizontal or vertical partitions would be sufficient (and they are useful as you can very quickly determine which side of a horizontal or vertical line the camera is on). However, this room demonstrated that such a limitation would not be practical.

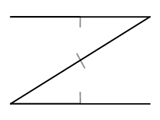
Consider the above geometry. The black lines are walls and the small grey lines represent the wall normals; that is, the walls face the inside of the "Z". The wall in the middle is double-sided; you could put the camera above or below it and see it. However you slice that map up with horizontal or vertical partitions you will still end up with regions that are not convex.

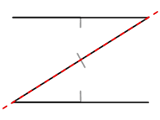
A single partition along the central wall divides the map into two convex regions. I had initially thought that checking which side of such a partition the camera lay would be an expensive operation, but it's not too bad; as a line can be represented by the expression y=mx+c I can store the gradient m and y-intercept c in the level data and simply plug in the camera's x and compare to y to determine the side. A single multiplication and an addition isn't too much to ask for.

Fortunately, there are only two of these partitions in the level!

I have added some other features to the demo program. Pressing Zoom when using a calculator that can run at 15MHz (a TI-83+ SE or any TI-84+) toggles the speed between 6MHz and 15MHz. Pressing Mode or X,T,Θ,n allows you to look up or down. Pressing Window toggles between the default free movement and a mode which snaps you to a fixed height above the floor. These additions are shown in the below screenshot (click to view the animation):

Unfortunately, performance is lousy. Viewing the stairs drops the framerate to a rather sluggish 6 FPS when running at 6MHz (most of the above screenshot is recorded at 15MHz). The LCD's natural motion blur helps a little (it feels a lot more fluid on the calculator than it does on a PC emulator) but I'm aiming for a minimum of 10 FPS, so I need to make quite a few optimisations. There are several low-level ones that could be made; for example, when clipping the 2D line segments to the display I'm using a generic line clipper that clips the line both horizontally and vertically. As wall has been clipped to the horizontal field of view by that point I only really need to clip it to the top and bottom edges of the display. There are also some high-level optimisations to be made; for example, double-sided walls are currently stored as two distinct walls with the vertex order swapped. This means that to handle both sides of the wall the engine has to clip and project it twice, which involves lots of expensive divisions and multiplications. The results of these operations could be cached so that they only needed to be calculated once.

A TI-83 and TI-83+ binary is available if you'd like to try the demonstration on your calculator: please download Nostromo.zip. The usual disclaimers about backing up your data before running the program apply!

Varying wall heights in a 3D engine for the TI-83+

Monday, 25th October 2010

I've done a little more work on the 3D engine for TI-83+ calculators that I mentioned in the previous entry. The main difference is in limited support for varying the heights of floors and ceilings, illustrated in the following screenshots.

    

    

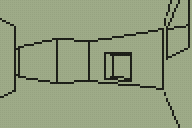
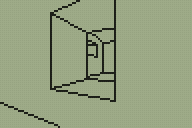
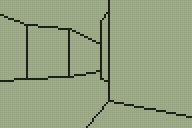
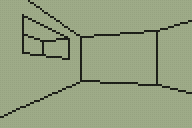
Walls now refer to one or two "sectors". A sector is a 2D region of the map of any size or shape; it can be concave or even have holes in it. Walls are also grouped into convex regions named subsectors for rendering purposes. Each wall has a sector in front of it and a sector behind it; these sectors have a specified floor and ceiling height. There are now two types of wall; a "middle" wall which connects the floor and ceiling of the sector in front of it and an "upper and lower" wall which connects the ceilings of the sectors on each side and the floors of the sectors on each side.

This makes occlusion a little trickier and determining where to draw lines around the edges of walls even more so!

    

The previous version of the renderer worked by drawing walls back-to-front, clearing rectangles the height of the screen behind the wall segments as they were drawn. The first attempt to improve this exchanged rectangles the full height of the screen with trapezia. The screenshot to the left shows the bounding rectangle around each wall segment being filled and the one to the right shows each wall filled as a trapezium. (As before, clicking an image with a border will display an animated screenshot).

    

Rather than attempt to calculate where lines should be drawn around wall edges I thought I'd experiment with dithered wall fills instead. The left screenshot shows this addition (each wall has a different shade) and the right screenshot shows the addition of support for wall heights (still drawn in the simple back-to-front technique, resulting in significant amounts of overdraw).

Unfortunately, the LCD on the calculator copes rather poorly with dithered fills; the above photograph was taken at the highest contrast setting. Rotating the camera to look at walls with a different dither pattern brings the world back into view. This is rather unacceptable, and is something I ran into with my previous implementation. I think I'll stick to stroked wall outlines rather than filled walls.

I had been experimenting with a new level design in the C# prototype of the engine that added another room accessible via a tunnel from the starting room. I added some code to the C# program to output the level data in a form that could be assembled into the Z80 version. This is shown above, having reverted to a simple wireframe view in anticipation of the new wall drawing code.

The new way to implement occlusion works very differently to the previous one. I had been sorting the geometry from back-to-front and rendering it in order, drawing walls in the foreground on top of walls in the background. This wasn't very efficient and wouldn't scale well. The new approach renders from the front to the back and works on information stored about each column of pixels on the screen. The screen is 96 pixels wide, so there are 96 columns to deal with. A counter is set to 96 at the start of rendering. When a column of a wall is rendered, a flag is set to indicate that that column has been completed and the counter is decremented. When the counter reaches zero, that means that every column on the screen has been completed and the renderer terminates. This is demonstrated in the above screenshot when compared to the previous one; walls that are some distance away from the camera (and behind other wall segments) are not always drawn as the renderer has decided that it has finished before reaching them.

An obvious issue with the above screenshot is that even though some of the geometry is culled, individual walls can still be seen through other ones.

Part of the solution is to use a custom line-drawing routine that checks each pixel against the completed columns table. If a column is marked as completed, the pixel is not drawn; if it isn't, the pixel is drawn. This is shown above.

I previously mentioned that there were two types of wall; "middle" walls (solid ones from the floor to the ceiling) and "upper and lower" ones (these have a hole in the middle). Only "middle" walls flag a column as being completed, as you need to be able to see through the hole in "upper and lower" ones. This causes the rendering bugs in the previous screenshot above and below the holes in the wall. The way to fix this is to add two new per-column clipping tables; one which defines the top edge of the screen and another which defines the bottom edge. These both start at the maximum values (0 for the top edge and 63 for the bottom) and are reduced whenever an "upper and lower" wall type is encountered.

The new code to do this is demonstrated in the above screenshot. There is still, however, a bug in this implementation. The per-column clipping tables are updated by the code that draws the line along the bottom or top edge of the hole in the wall. If this line is partially (or completely) off the screen, these tables are not updated and the rendering bugs appear again (as demonstrated at the end of the above screenshot). A final manual pass over parts of the line that are clipped off the screen corrects the issue:

As can be seen in the bottom left corner of the above screenshot I have added an FPS counter. This is accompanied by code that scales movement by elapsed time so you move at the same speed regardless of how long each frame takes to render. The engine is quite slow (and could no doubt be heavily optimised by someone who's good at assembly) and has quite a few bugs in it but it's certainly looking a little better than it did a week ago. As I only have a regular TI-83+ I'm aiming for something usable at 6MHz; the more modern calculators can run at 15MHz but this feature is not used in the demo.

Download Nostromo.zip

For those interested in trying the demo on their calculators, click on the above image to download an archive containing a TI-83+ and TI-83 binary. As before, this is experimental and may well crash your calculator, so please back up any important files first!

A primitive 3D engine for the TI-83+

Sunday, 17th October 2010

As you may have guessed from the number of spinning cubes in my projects, I am quite fond of primitive 3D. As you may also have guessed from the number of TI-83+ calculator projects I have undertaken, I'm also quite fond of programming on low-end machines. I have never really successfully put 3D and the TI-83+ together, though.

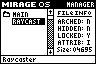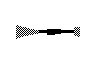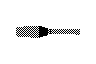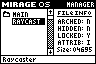
One way to build a 3D world in software is raycasting (e.g. Wolfenstein 3D). This typically results in blocky worlds where all walls are at 90° angles to each other. There are several games using raycasting engines on the TI-83+ already; they are much faster and better-looking than my sorry attempt pictured above.

Another method is to use true 3D geometry (e.g. Quake). Many years ago I attempted to work on something that looked a little like Quake. I built this on the Matt3D engine, which supported basic 8-bit coordinates and lines, but not solid objects. The result was even less useful than the above raycaster!

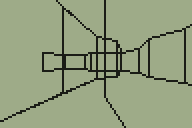
Another method somewhere between the two is a "2.5D" engine, where level geometry is defined between points in 2D space but projected in 3D (e.g. DOOM). This allows for walls that are not at 90° angles to each other, whilst simplifying the rendering procedure significantly. I spent some weeks working on such an engine a few years ago yet never managed to get any further than the above screenshot. As you can probably tell from the fact that you can see the walls through each other I never found a good way to handle occlusion, and the project ended up stagnating.

    

    

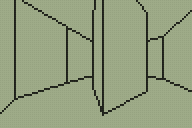
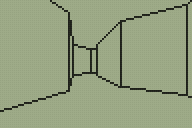
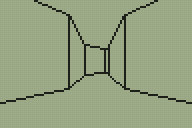
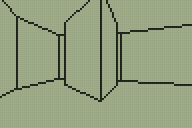
Looking for a quick weekend project I thought back to the work I'd done with the DOOM and Quake engines. These engines use a BSP tree structure to sort the level geometry for rendering. I reckoned that if simplified a little a similar tree structure could be used to render a 3D world on the TI-83+ calculator. The four screenshots above show that this technique is indeed quite successful. My implementation could certainly do with a lot of work but I think the theory is at least sound.

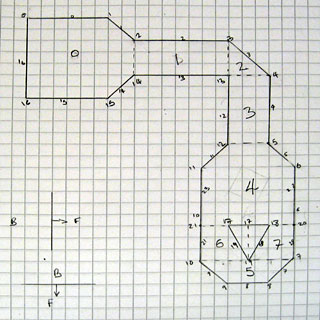
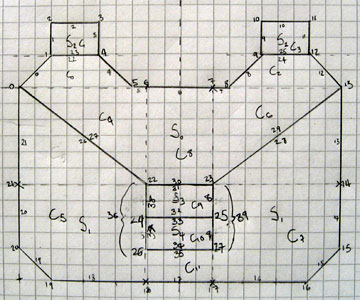
I decided that one way to make this project a bit more fun was to set myself a challenge; to design a level that I would, ultimately, be able to walk around in. This level is shown above, and contains a number of walls that are not parallel to the X or Y axis and a pillar. I have split the world into eight convex "sectors" (labelled 0 to 7) with a dotted line between them to show where the BSP tree is partitioned. All of the partitions are either horizontal or vertical to speed up tree traversal; the TI-83+'s Z80 CPU does not support floating point arithmetic, let alone multiplication or division, so being able to decide which side of a partition you're on quickly is very useful.

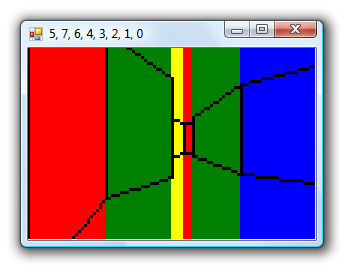
Rather than dive straight into Z80 assembly programming I knocked together a quick prototype in C#. This allows for quick and easy debugging; the blocks of colour allow me to quickly identify walls and the application title bar contains the order in which the sectors have been rendered. These can then be checked against the version running on the TI-83+ in case there are problems.

With the C# version running satisfactorily I started converting it to Z80 assembly. The above screenshot shows the first step; transforming the level's vertices around the camera. Clicking on the screenshots will take you to an animated version; as some of them are quite large I have linked to them rather than embedding them directly.

The next step was to traverse the BSP tree. The numbers across the top of the screen indicate the order in which to render the sectors, from back to front — however, due to a simple bug, they are actually listed from front to back. This was fortunately very easy to fix.

Walls are connected between the vertices, so I quickly threw something together to display all of the walls on the screen. The walls will have to be clipped against the camera's view (or discarded entirely if they are outside the view) so being able to see them is a great debugging aid!

We are only interested in drawing walls that are in front of the camera, so the first bit of clipping code deals with clipping the walls against Y=0.

        

The above screenshots show the final three stages of clipping to the camera's view, defined by Y>0, Y>+X and Y>-X. The first screenshot shows culling of any wall that does not satisfy this in any way; walls that are completely outside the view are discarded. The second screenshot shows walls being clipped against Y=+X, and the third finally adds clipping against Y=-X. The lack of hardware floating-point arithmetic makes the code fairly slow and ugly but it does seem to be working relatively well.

We are only really interested in dealing with walls that are facing the camera; we don't want to draw the back of walls. To work out which we want to keep and which we want to ignore, we project the wall to the screen and check whether its projected start vertex appears to the left or the right of its end vertex.

     

A simple perspective projection is performed to turn this clipped 2D world into what appears to be a 3D one. The X coordinate of each vertex is divided by its Y to get the X coordinate on-screen and the height of the wall is divided by the vertex Y to get the Y coordinate on-screen. The left screenshot shows the top and bottom of wall edges; the right screenshot adds lines between the floor and the ceiling to produce a more convincing "wireframe" view of the world.

The final step is to make the world appear solid, by hiding walls that are far away behind walls that are closer to us. Traversing the BSP tree gives us the order in which to draw the walls, so all that is required is to draw solid quadrilaterals for each wall rather than the lines around its outside. A fast clipped quadrilateral filler would take me some time to write so I cheated by drawing a solid white rectangle the width of the wall and the height of the entire screen before drawing the wall outlines. As the camera is half-way up each wall and all of the walls are the same height there are no cases where a foreground wall only partially covers a background one so this trick works for the time being.

I'm glad I achieved my goal of walking around the 3D world I'd sketched in pencil at the start of the weekend but I'm not sure where I'll be able to take the project now. Turning it into a useful 3D engine for a game would certainly require a lot of work. The level and its BSP tree were generated by hand, which would not lend itself well to anything but the simplest of levels. However, the lack of variation in wall heights produces fairly dull levels in any case; DOOM-style levels would be something to strive for, but I'm not sure how well the calculator would be able to cope with them. I'm also unsure how well the engine would scale; this very primitive version only achieves around 12 FPS on a 6MHz TI-83+. It's certainly given me something interesting to think about!

If you would like to try the program on your calculator, please download Nostromo.8xp. It requires an Ion-compatible shell to run. It is very primitive, likely to be quite buggy (you may encounter rendering bugs when very close to walls due to integer overflow in the clipping and projection code) and may well crash your calculator; please back up any important files before running it. Use the arrow keys to move around, Trace and Graph to strafe and Clear to quit.